Coxeter, Escher, and Whiteley: Geometry, Art, and the Role of Visualization

repare for a true blog post, quick and dirty. But the Boston Globe ran a great piece on Sunday about Donald Coxeter, The Man Who Saved Geometry. As it turns out, this article is right up the alley of Think In Pictures in that it paints a portrait of an academic climate in which visualization is finally coming to be seen as equal partner with language in a field's development and its outreach efforts, so I wanted to dash off a few comments about the article. (If you aren't registered with the Globe's website, borrow one of these usernames and passwords from Bugmenot.)

The article first describes the disrepute into which the study of geometry had fallen before Coxeter came along, instigated by a group that wrote under the collective pen name of Nicolas Bourbakis:

The Bourbakis espoused mathematical rationality and rigor. They believed the subjective and fallible visual sense was easily led astray, falling victim to impressionistic reasoning. In 1959, at a conference in France addressing the need to overhaul the French education system, Jean Dieudonne, a founding member of the Bourbakis and the group's scribe, infamously proclaimed: "Down with Euclid! Death to Triangles!"

Eventually, the Bourbakis way of mathematics pervaded the Western world, reaching even into grade schools with the Sputnik-motivated New Math reforms of the 1960s, which aimed to improve students' performance and to ensure America was not left in the scientific dust by the Soviet Union. Instead of shapes, children studied axioms and set theory.

As a consequence, mathematical and scientific investigation suffered from what Walter Whiteley, a great admirer of Coxeter and director of applied mathematics at York University in Toronto, calls the "geometry gap." Whiteley's thesis holds that when the areas of the brain that process visual and geometric concepts fall into disuse, the realms of mathematics and science suffer as well.

Coxeter responded to this challenge through a variety of means, including lecturing, collaboration with artists, and the development of new tools and applications for geometry. Of course, the connection to art interests me most. (I must admit, I hated geometry in high school.) Beginning in the 1950s, the Globe reports, Coxeter worked closely with M.C. Escher, who had no mathematical background, to help the artist visualize the concept of infinity in many of Escher's works.


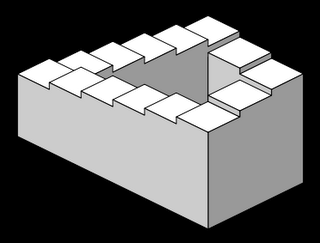
The craftily-structured paragraph seems to insinuate that Coxeter's mathematics contributed to Escher's "Ascending and Descending" infinite staircase, which is incorrect. This form was developed by Lionel and Roger Penrose and published in 1958; much of the groundwork in optical illusions was done by Oscar Reutersvard in the 1930s, but was probably not known to these later mathematicians, or to Escher himself.

Even more relevant to themes frequently touched on in this blog, the battle between geometry and algebra seems to be a phenotype of a purer tension between the expressive modes of language and visualization. The Globe makes the tantalizing connection:

The visual and the algebraic perspectives are in constant flux in the mathematical and scientific disciplines. "The battle between geometry and algebra is like the battle between the sexes," said Sir Michael Atiyah, honorary professor of mathematics at Edinburgh University. "It's the kind of problem that never disappears. It'll never be dead, and it will never get solved. The question is, 'What is the right balance?"'

"It goes back and forth, and not in an accidental way," said Peter Galison, professor of the history of science and physics at Harvard. "Pushing hard on the visual methods ends up pushing toward the antivisual. Beliefs swing between an almost theological dogma that images are stepping stones to higher knowledge, or that they are deceptive idols that keep us from higher understanding."

In the design of educational materials - I will speak specifically about PowerPoint, which I use every day, but the same applies to Flash, web pages, or any other medium that involves the use of sequential visuals - this tension is often resolved in a way that makes the best use of both written and visual channels: illustrative diagrams that are just complex enough for the purpose at hand, or words that accompany pictures to create meaning that neither alone could communicate as effectively, for example.

But this harmony involves a case-by-case negotiation of a topic's text/visual balance that places it along a continuum, not at a predetermined set of values. There is no single right answer for how much of your explanation of a topic should be text, and how much image, and how the two should relate; in each case, factors include how much a topical visual can clearly show, how much text can do to help explain and/or place a visual in an essential context, and how much of the language involved (in PowerPoint at least) should be shared orally by a speaker rather than being written out. Cases where text should predominate tend (in my experience) to be cases where there is a strong narrative thread linking information together, and the logic of the narrative is the strongest means of reaching a student. However, even in many of these cases, a few words can go a long way, and visuals can dominate the slide.

The article got me very interested in Whiteley, and his home page at York University a fascinating report he wrote with several others for a SIGGRAPH conference, which covers a lot of ground regarding how and why students in the sciences should be thrust into some visualization and design challenges both to broaden their thinking and to prepare them to communicate the results of their work effectively. The paper includes a number of idea-packed lists (one of which discusses the role of narrative in learning, which gels with my own impressions offered above), and would be worth skimming solely on the strength of these aphoristic minefields even if the paper wasn't so interesting. One of my favorites of these is excerpted below, with points bolded which I find to be particularly difficult obstacles for "right-brained" people to appreciate when creating teaching materials for K-12 students (or any other general audience):

Basic misconceptions about visual perception and communication

• We see what is there.
• You see what I see.
• Mind and consciousness are the same.
• Reason is the primary cognitive experience.
• The tools for analyzing and understanding linguistic and logical processes are adequate for analyzing and understanding visual processes.
• If you are not conscious of using visual perception, you are not using it.
• I cannot be held responsible for unintended consequences of my use of visual media.
• Visual media has no effect on me. I can control the effect of visual media.
• Three-dimensional understanding is built from two-dimensional understanding.
• Visuals are trivial - you either get them or you don't.
• Visuals are hard - if you don't get them, there is nothing you can do.